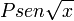
Usaremos o método da primitivação por substituição e da primitivação por partes.
Façamos a seguinte substituição: 

Temos então que:
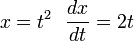
Substituindo ficamos então com: 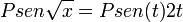
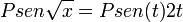
Aplicamos agora a primitivação por partes
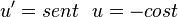
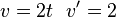
Psen(t)2t = − cos(t)2t − P2( − cos(t)) = − cos(t)2t + 2Pcos(t) =
= − cos(t)2t + 2.sen(t) + C = 2( − t.cos(t) + sen(t)) + C
fazendo agora a substituição inicial 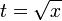 temos o resultado final:
temos o resultado final:
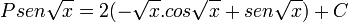
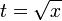 temos o resultado final:
temos o resultado final: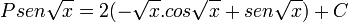

Sem comentários:
Enviar um comentário