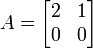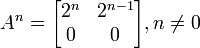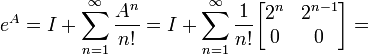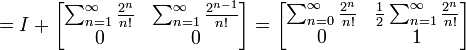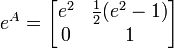Deparei-me com esta primitiva num exame de Matemática de um amigo meu da Universidade Nova de Lisboa. Com algumas manipulações trigonométricas e aplicando a primitivação por partes duas vezes, é possível chegar ao resultado pretendido.
Antes de mais é necessário separar os dois termos no quadrado e ter em consideração algumas igualdades trigonométricas
Podemos agora começar a primitivar a equação tendo em conta esta igualdade trigonométrica, pois conseguimos eliminar o quadrado do seno. Sendo assim ficamos com
A primitiva de x² é imediata. Para primitivar x²cos(2x) teremos que recorrer à primitivação por partes, ou seja
Quando primitivamos por partes temos de saber qual o termo que derivamos e qual o termo que primitivamos. Na fórmula acima mencionada primitivamos (v') pois ficamos com (v) e derivamos (u) pois ficamos com (u'). Neste caso vamos derivar o termos x² e primitivar o termo cos(2x)
Aplicamos novamente o método da primitivação por partes
Finalizando ficamos com
Resolução do Exame de Matemática da UAL de 18 de Janeiro de 2010
terça-feira, janeiro 26, 2010
, publicada por
João Pimentel Ferreira
Coloco aqui para apreciação e crítica a resolução do Exame de Matemática da UAL de 18 de Janeiro de 2010 para a Licenciatura em Gestão Diurna.
Qualquer errata, sugestão, opinião ou dúvida pode deixar um comentário que tentarei ser breve na resposta.
Visualizar o exame resolvido
Qualquer errata, sugestão, opinião ou dúvida pode deixar um comentário que tentarei ser breve na resposta.
Visualizar o exame resolvido
Como distinguir Arranjos completos, Arranjos simples e Combinações?
segunda-feira, janeiro 25, 2010
, publicada por
João Pimentel Ferreira
Muitos alunos ficam perplexos e atónitos quando se deparam com a matéria em que é necessário distinguir estes três casos. Quando aplicar os Arranjos completos, os arranjos simples ou as combinações?
Para responder a esta questão elaborarei três casos paradigmáticos:
- O código do Multibanco
- O almoço das quatro amigas
- O euromilhões
- O código do multibanco
- Arranjos completos
- Arranjos completos
Quantos de nós têm de escolher um código para efectuar operações com o multibanco. Um código é-nos dado, mas podemos alterá-lo quando quisermos. Mas quantos códigos podemos escolher?
Temos quatro dígitos, onde em cada dígito podemos escolher de entre dez números, do zero ao nove; o zero também conta pois também podemos escolhê-lo. Podemos repetir os algarismos o número de vezes que quisermos, pois os códigos 1111 e 5544 são válidos, em que no primeiro caso temos o 1 repetido e no segundo caso repetimos o 5 e o 4. E a ordem conta, ou seja, o código 1234 é diferente do 4321.
Então quando há repetição e a ordem conta estamos perante Arranjos Completos
No caso do multibanco temos arranjos de dez, quatro a quatro. A fórmula geral é dada no seguimento
Podemos escolher então de entre dez mil códigos multibanco possíveis. Em qualquer palavra-passe onde se possam repetir os caracteres e onde a ordem pelos quais os caracteres estão ordenados seja preponderante, pode-se aplicar os arranjos completos.
- O almoço das quatro amigas
- Arranjos simples
- Arranjos simples
A Rita, a Patrícia, a Joana e a Andreia decidem ir almoçar.
A mesa é quadrada e tem quatro lugares distintos. De quantas maneiras diferentes se podem sentar as quatro amigas? Podemos sentar a Rita em quatro lugares distintos, mas assim que escolhermos um lugar para a Rita esse lugar ficará dado e ocupado.
E bem sabemos como são as mulheres no que concerne ao lugar onde se irão sentar, como tal a ordem pela qual vão ficar sentadas conta. A Andreia sentar-se no lugar em frente à janela é diferente de sentar-se no lugar ao lado da casa-de-banho. E lembremo-nos que Rita, só há uma. A Rita não se repete, logo neste caso não existe repetição.
Resumindo, temos quatro amigas para quatro cadeiras, onde a ordem conta e não há repetição. A ordem conta porque sentá-las em locais diferentes, resulta em casos diferentes, e não há repetição, pois Patrícia no almoço, só há uma.
Temos então Arranjos simples de quatro elementos quatro a quatro
Temos então vinte e quatro maneiras diferente de sentar quatro amigas num almoço de confraternização. Lembremo-nos que 0! = 1
Nos Arranjos simples a ordem conta e não há repetição.
Resumindo, no caso paradigmático das quatro amigas, estamos perante Arranjos simples.
- O euromilhões
- Combinações
- Combinações
Foquemo-nos somente nas estrelas do Euromilhões. Podemos escolher duas estrelas de entre nove números tal como refere a imagem.
De quantas maneiras diferentes podemos escolher duas estrelas de entre nove números no euromilhões? A partir do momento em que escolhemos a estrela número dois, já não podemos voltar a escolhê-la, logo não existe repetição. E escolher em primeiro lugar a estrela número dois e depois escolher a estrela número nove, ou vice-versa, é completamente indiferente, logo a ordem não conta.
Quando a ordem não conta e não existe repetição estamos perante Combinações que tem como caso paradigmático o Euromilhões. Neste caso teríamos combinações de nove elementos dois a dois.
Existem então trinta e seis maneiras diferentes de preencher as estrelas no Euromilhões. Quando não há repetição e a ordem não conta, estamos perante Combinações.
______________________________
Resumindo
Arranjos Completos (A') - Há repetição, a Ordem conta
Arranjos Simples (A) - Não há repetição, a Ordem conta
Combinações (C) - Não há repetição, a Ordem não conta
_____________________________
Resumindo
Arranjos Completos (A') - Há repetição, a Ordem conta
Arranjos Simples (A) - Não há repetição, a Ordem conta
Combinações (C) - Não há repetição, a Ordem não conta
_____________________________
Todos os outros casos mais complexos que possamos ter, são uniões de vários casos destes acima referidos, ou uniões de casos diferentes. É preciso saber qual das situações aplicar, se Arranjos Completos, Arranjos simples ou Combinações, tendo em conta se há ou não repetição ou se a ordem conta ou não. Para cada um destes casos temos um caso paradigmático do quotidiano de cada um que pode ser aplicado.
Resolução do Exame de Matemática I do ISCTE de 11 de Janeiro de 2010
domingo, janeiro 24, 2010
, publicada por
João Pimentel Ferreira
Coloco aqui para apreciação e esclarecimento se possível, o enunciado e a resolução do exame do ISCTE de Matemática I leccionado a diversos cursos da faculdade. O exame foi realizado no dia 11 de Janeiro de 2010.
Creio que todas as questões estão respondidas correctamente segundo critérios matemáticos rigorosos. Qualquer comentário, errata, sugestão, opinião ou dúvida por favor deixe um comentário que tentarei ser breve na resposta.
Pode visualizar o enunciado ou a resolução
Creio que todas as questões estão respondidas correctamente segundo critérios matemáticos rigorosos. Qualquer comentário, errata, sugestão, opinião ou dúvida por favor deixe um comentário que tentarei ser breve na resposta.
Pode visualizar o enunciado ou a resolução
Calculadoras Autorizadas para os Exames Nacionais de Matemática A e B
quarta-feira, janeiro 20, 2010
, publicada por
João Pimentel Ferreira
Lista exemplificativa, não exaustiva, de máquinas de calcular gráficas passíveis de serem utilizadas nos exames nacionais de Matemática A, Matemática B e Matemática Aplicada às Ciências Sociais.
| Casio | Texas Instruments | Sharp | Lexibook | |
| FX-6300 G | FX-9750 GA Plus | TI-80 | EL-9400 | GC 500 |
| FX-6900 G | FX-9860 G | TI-81 | EL-9600/9650 | GC 1000 |
| FX-6910 AG | FX-9860 G SD | TI-82 | EL-9900 | GC 1500 |
| FX-7000 G | FX-9860 G Slim | TI-82 STATS | GC 2000 | |
| FX-7000 GA | FX-1.0 | TI-83 | ||
| FX-7200 G | FX-1.0 Plus | TI-83 Plus | ||
| FX-7300 G | CFX-9800 G | TI-83 Plus SE | ||
| FX-7400 G | CFX-9850 G | TI-84 Plus | ||
| FX-7400 G Plus | CFX-9850 G Plus | TI-84 Plus SE | ||
| FX-7450 G | CFX-9850 GB Plus | TI-85 | ||
| FX-7500 G | CFX-9850 GC Plus | TI-86 | ||
| FX-7700 G | CFX-9940 GT | TI-Nspire | ||
| FX-7700 GB | CFX-9950 G | |||
| FX-7700 GE | CFX-9960 G Plus | |||
| FX-7700 GH | CFX-9950 GB Plus | |||
| FX-7900 GC | CFX-9960 GT | |||
| FX-8500 G | GRAPH 20 | |||
| FX-8700 G | GRAPH 25 | |||
| FX-8930 GT | GRAPH 35 | |||
| FX-9700 GE | GRAPH 65 | |||
| FX-9700 GH | GRAPH 85 | |||
| FX-9750 G | GRAPH 85 SD | |||
| FX-9750 G Plus | ||||
Podem algumas máquinas não estar nesta lista, já que não é uma lista exaustiva, é apenas exemplificativa.
Para serem autorizadas as máquinas devem cumprir cumulativamente todas estas características:
- serem silenciosas
- não necessitarem de alimentação exterior localizada
- não terem cálculo simbólico (CAS)
- não terem capacidade de comunicação à distância
- não terem fitas, rolos de papel ou outro meio impresso
Tabela de Primitivas e Integrais
terça-feira, janeiro 19, 2010
, publicada por
João Pimentel Ferreira
Aqui coloco uma pequena tabela com as derivadas mais comuns
A fracção d/dx é uma notação equivalente a f '(x). De salientar que a variável x não é uma função x(t), limitando-se a ser simplesmente uma variável simples x, para os casos em que x depende de t, ou seja x(t), basta aplicar a derivada da função composta.
Agora uma tabela com os integrais mais comuns
De salientar que a tabela acima mencionada refere integrais indefinidos, para integrais definidos bastará aplicar o Teorema fundamental do Cálculo
A fracção d/dx é uma notação equivalente a f '(x). De salientar que a variável x não é uma função x(t), limitando-se a ser simplesmente uma variável simples x, para os casos em que x depende de t, ou seja x(t), basta aplicar a derivada da função composta.
Agora uma tabela com os integrais mais comuns
De salientar que a tabela acima mencionada refere integrais indefinidos, para integrais definidos bastará aplicar o Teorema fundamental do Cálculo
Pequenos memorandos para manipulação algébrica
sábado, janeiro 16, 2010
, publicada por
João Pimentel Ferreira
Aqui coloco alguns memorandos para facilitação na manipulação de expressões algébricas.
Começo pelos mais simples, no que refere à multiplicação e divisão de fracções
Agora ligeiramente mais elaborados, estes referem-se às raízes e expoentes
Estes pequenos memorandos para manipulação algébrica são realmente fundamentais para os alunos que aprendem matemática ao nível secundário e superior
Será que o gelo depois de derretido faz aumentar o nível da água?
sábado, janeiro 16, 2010
, publicada por
João Pimentel Ferreira
Colocaram-me, em tempos quando fui a uma entrevista de emprego o seguinte problema, imagine um recipiente com água, e no topo do recipiente encontra-se um cubo de gelo a flutuar, quando o gelo derreter como é que se alterará o nível da água? Manter-se-á? Aumentará ou diminuirá?
Custou-me a responder, e por certo que o entrevistador queria que eu tivesse uma noção sobre a alteração do estado da matéria e como tal, que me fosse intuitivo a alteração do volume dos objectos quando mudam de estado físico. O gelo embebido na água alterará o nível da água quando este derreter? Eu sabia que o gelo é menos denso que a água, e é por este mesmo facto que flutua, como tal haveria de ocupar mais espaço. Pensei à primeira vista que talvez o nível aumentasse devido a este facto.
Mas ao derreter lentamente, o cubo ao tornar-se mais leve, também haveria de ocupar menos espaço dentro de água, o que faria com que a água não subisse tanto, reflecti eu. Talvez este factor fosse compensador, e fizesse com que o nível da água se mantivesse. Iria dar a resposta sobre a qual havia reflectido: mantém-se. Mas de súbito, surgiu um dado empírico. Sempre ouvi dizer que o derretimento das calotas polares devido às alterações climáticas provocavam o aumento do nível médio da água do mar. Então a resposta que dei foi: aumenta.
Foi mais um dos casos em que deixei que os dados empíricos se sobrepusessem à intuição racional, e tal revelou-se num pensamento de cariz falacioso. Cheguei a casa e tentei aferir matemática e fisicamente através da álgebra qual o resultado correcto. Exponho aqui esse raciocínio:
Imaginemos um cubo de gelo de lado x que está emergido num recipiente com água. A base do recipiente é um quadrado de lado y. O gelo, suponhamos, tem apenas uma fracção de altura a emergida na água. A altura da água no estado inicial é hi . Depois do gelo derreter completamente, encontramo-nos no estado final, em que obviamente o recipiente é o mesmo, e em que teremos uma altura de água hf.
A figura seguinte tenta ser representativa daquilo que refiro:
É sabido que a densidade de um objecto é a sua massa sobre o seu volume
Pela lei de Arquimedes um corpo flutua quando o seu peso é igual ao peso de líquido deslocado onde flutua, ou seja neste caso
(2)
Em que MG é a massa do cubo de gelo, Mágua deslocada é a massa da água deslocada, g é a aceleração gravítica, ρg é a densidade do gelo, ρa é da densidade da água, x é o comprimento do lado do cubo de gelo e a é a porção de gelo que está submersa tal como está indicado na figura acima representada. Simplificando a fórmula acima descrita obtemos:
(3)
É sabido que depois do gelo derreter, a água daí resultante se mistura com a água inicial já existente no recipiente. Significa que a massa de gelo mais a massa de água inicial será igual à massa de água total no estado final, ou seja:
(4)
Nesta equação Ma é a massa de água inicial, MG é a massa do cubo de gelo e Mf é a massa total final depois do cubo de gelo derreter completamente. Desenvolvendo esta equação sabendo a equação em (1) e tendo em consideração a figura representada obtemos
Substituindo nesta equação, a variável a da equação (3), obtêm-se:
Conclui-se assim que a altura final é igual à inicial. Ou seja o derretimento do gelo quando está a flutuar, não provoca qualquer aumento no nível da água. É que a água é um dos raros elementos cujo estado sólido é menos denso que o seu estado líquido, por isso é que o gelo flutua. Simplificando, neste caso, o gelo ao derreter, faz com que a sua água equivalente vá ocupar exactamente o espaço que o gelo tinha embebido dentro da água do recipiente, verificando assim o princípio de Arquimedes. Este raciocínio poderá ser aplicado a todas as matérias que flutuem em que o objeto que flutua é do mesmo elemento que o líquido onde está embebido e que tenham as mesmas densidades antes e depois do derretimento, ou seja, da fusão do sólido. A flutuação só acontece quando o sólido é menos denso que o líquido.
O derretimento das calotas polares provoca o aumento do nível médio do mar, primeiramente porque uma grande parte do gelo em causa, como na Antártida ou na Gronelândia, está assente em rocha e não está a flutuar. Em segundo lugar, considerou-se no exercício, que a densidade da água depois do gelo derretido, e a densidade de água do recipiente antes do gelo derreter, eram a mesma, o que nem sempre é o caso. Caso consideremos densidades diferentes antes e depois do gelo derreter, ou seja ρ'a para a densidade inicial da água e ρa para a densidade final da água na equação (5) teremos:
o que resulta em:
onde ρ'a é a densidade inicial da água e ρa é a densidade final da água. Como muito do gelo que está a flutuar é composto por água mais doce em comparação à água do mar, tal resulta que 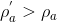 e por conseguinte justifica-se o aumento do nível do mar, pois resulta da inequação anterior que:
e por conseguinte justifica-se o aumento do nível do mar, pois resulta da inequação anterior que:
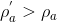 e por conseguinte justifica-se o aumento do nível do mar, pois resulta da inequação anterior que:
e por conseguinte justifica-se o aumento do nível do mar, pois resulta da inequação anterior que:Pequena apresentação | Mural do Mérito
sexta-feira, janeiro 15, 2010
, publicada por
João Pimentel Ferreira
João Pimentel Ferreira licenciou-se pelo Instituto Superior Técnico em Engenharia Electrotécnica e de Computadores, tendo estudado um ano no Instituto Real de Tecnologia em Estocolmo. Teve sempre diversas cadeiras ao longo do curso relacionadas com a Matemática, nomeadamente quatro análises matemáticas, álgebras, análise numérica, probabilidade e estatística e controlo linear, referindo ainda que em todo o curso a Matemática esteve presente. Em 1993 foi um dos cinco premiados nas XI Olimpíadas Nacionais de Matemática.
José Maria Sousa licenciou-se com distinção pelo Instituto Superior Técnico em Engenharia Electrotécnica e de Computadores, tendo estudado um ano na Universidade Norueguesa de Ciência e Tecnologia em Trondaime. Está neste momento como doutorando na investigação de sistemas de navegação e sistemas inérciais.
______________
Temos vários anos de experiência na explicação de Matemática, visto darmos explicações desde os tempos iniciais da faculdade e estamos a par dos diversos programas curriculares, dos diferentes anos lectivos e de diferentes faculdades e Universidades. Não somos um centro de explicações convencional, somos um grupo de explicadores que se reuniu em torno de um projeto comum de promover a matemática junto do espaço cibernético.
Damos explicações individuais ou com dois alunos, nas nossas residências, do 10º ano à faculdade, envolvendo todas as matérias relacionadas com a Matemática nos respectivos anos de ensino.
Fazemos também preparação para o exame nacional do 12º ano tendo a diversa bibliografia recomendada pelo Ministério da Educação. Também resolvemos exames e exercícios a pedido. Quaisquer dúvidas ou exercícios pontuais que tenha, respondemos gratuitamente no fórum.
Estamos presentes em Braço de Prata e Areeiro.
_____________________
Apresentamos um Portefólio de Explicandos não exaustivo aos quais lecionámos durante um período mais alargado cadeiras de Matemática, tendo no entanto lecionado muitas outras explicações, no âmbito de dúvidas esporádicas e trabalhos para faculdade.
Mural do Mérito
Nome do Aluno
|
Contacto
|
Faculdade
|
Curso
|
Cadeira
|
Avaliação
|
Ana Carla
Pascoal
|
UAL
|
Gestão
|
Matemática
|
Aprovada
| |
Diogo Garcia
|
UAL
|
Gestão
|
Matemática
|
Aprovado
| |
Ana Elisa
Alves
|
Faculdade de
Arquitectura da UTL
|
Arquitectura
|
Matemática
|
Aprovada
| |
Filipe Rodrigues
|
ISEL
|
Engenharia
Mecânica
|
Álgebra Linear
e Geometria
Analítica
|
Aprovado
| |
Análise
Matemática I
|
Aprovado
| ||||
Gilberto Outeiro
|
ISCTE
|
Gestão e
Engenharia
Industrial
|
Matemática
|
Aprovado
| |
João Viana
|
FCT UNL
|
Engenharia
Electrotécnica
e de
Computadores
|
Álgebra Linear
e Geometria
Analítica
|
Aprovado
| |
André Sousa
|
ISCTE
|
Economia
|
Matemática I
| Aprovado | |
Liliana
Rodrigues |
|
ISCTE
|
Gestão
|
Optimização
|
Aprovada
|
Matemática
|
Aprovada
| ||||
Miguel Coelho
|
|
ISEL
|
Engenharia
Informática |
Álgebra Linear e
Geometria Analítica |
Aprovado
|
Matemática I
|
Aprovado
| ||||
Jerónimo Saleiro
|
12º ano
|
12º ano
|
Matemática A
| Aprovado | |
David Bronze
|
ISEL
|
Engenharia
Mecânica |
Análise
Matemática | Aprovado | |
Sara Moniz
|
12º ano
|
12º ano
|
Matemática A
| Aprovado | |
João
Pedro Costa |
|
12º ano
IST |
Engenharia
Mecânica |
Matemática A
|
Aprovado
|
Álgebra Linear
|
Aprovado
| ||||
Cálculo
Diferencial e Integral |
Aprovado
| ||||
Tânia Guerreiro
|
ISGB
|
Gestão
Bancária |
Matemática
| Aprovada | |
Pedro Nunes
|
ISEL
|
Engenharia Electrotécnica
|
Matemática Aplicada à Engenharia Electrotécnica
| Aprovado | |
Marco Franco
|
12º ano
|
12º ano
|
Matemática B
| Aprovado | |
Helena
Bouças |
|
FCT UNL
|
Engenharia
Mecânica |
Álgebra Linear
|
Aprovada
|
Análise Matemática I
|
Aprovada
| ||||
Jerónimo Saleiro
|
12º ano
|
12º ano
|
Matemática A
| Aprovado | |
João
Caleiro |
ISEL
|
Engenharia Civil
|
Álgebra Linear e
Geometria Analítica | Aprovado | |
Diana
Mendes |
ESTeSL
|
Saúde Ambiental
|
Matemática Aplicada
| Aprovada | |
Cristovão
Santos |
FCT UNL
|
Engenharia
do Ambiente |
Análise Matemática III
| Aprovado | |
Ivo
Fernandes |
FC UL
|
Engenharia
Informática |
Cálculo I
| Aprovado | |
João
do Vale |
Academia
Militar |
Curso de
Oficial |
Álgebra Linear
| Aprovado |
Obrigado pela sua visita à Matemática Viva
Cálculo da exponencial de uma matriz
sexta-feira, janeiro 01, 2010
, publicada por
João Pimentel Ferreira
Em matemática, a exponencial de uma matriz é uma função matricial definida no conjunto das matrizes quadradas e possui propriedades semelhantes função exponencial definida nos números reais (ou complexos). Mais abstratamente falando a exponencial matricial estabelece uma conexão entre a álgebra de Liedas matrizes e o seu correspondente grupo de Lie.
Seja  uma matriz real ou complexa
uma matriz real ou complexa 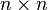 , define-se
, define-se  pela seguinte série de potências:
pela seguinte série de potências:
 uma matriz real ou complexa
uma matriz real ou complexa 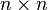 , define-se
, define-se  pela seguinte série de potências:
pela seguinte série de potências: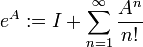 , onde
, onde  é a matriz identidade
é a matriz identidade
A convergência desta série é garantida pelo teste M de Weierstrass.
Propriedades
Sejam  e
e 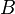 matrizes quadradas
matrizes quadradas 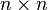 e
e  e
e  números reais ou complexos arbitrários. Denotamos por
números reais ou complexos arbitrários. Denotamos por  a matriz identidade
a matriz identidade 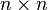 e por
e por 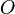 a matriz nula de mesmas dimensões.
a matriz nula de mesmas dimensões. 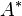 indica a matriz transposta conjugada de
indica a matriz transposta conjugada de  e
e 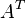 denota a matriz transposta de
denota a matriz transposta de  . São válidas as seguintes propriedades:
. São válidas as seguintes propriedades:
 e
e 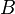 matrizes quadradas
matrizes quadradas 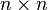 e
e  e
e  números reais ou complexos arbitrários. Denotamos por
números reais ou complexos arbitrários. Denotamos por  a matriz identidade
a matriz identidade 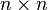 e por
e por 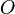 a matriz nula de mesmas dimensões.
a matriz nula de mesmas dimensões. 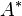 indica a matriz transposta conjugada de
indica a matriz transposta conjugada de  e
e 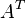 denota a matriz transposta de
denota a matriz transposta de  . São válidas as seguintes propriedades:
. São válidas as seguintes propriedades: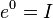
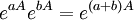
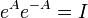
- Se
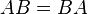 então
então 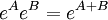
- Se
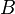 é uma matriz invertível então
é uma matriz invertível então 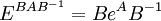
 , onde
, onde 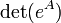 é o determinante de
é o determinante de 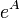 e
e 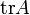 é o traço de
é o traço de 
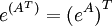 . Disto segue que se
. Disto segue que se  é uma matriz simétrica
é uma matriz simétrica 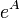 também o é. Se
também o é. Se  é uma matriz anti-simétrica é uma matriz ortogonal.
é uma matriz anti-simétrica é uma matriz ortogonal. . Disto segue que se
. Disto segue que se  é uma matriz hermitiana
é uma matriz hermitiana 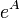 também o é. Se
também o é. Se  é uma matriz anti-hermitiana é uma matriz unitária.
é uma matriz anti-hermitiana é uma matriz unitária.
Exemplo no cálculo da exponencial de uma matriz
Imaginemos que queremos calcular eA sabendo que
Calculemos A2,A3...An
Sabemos então que
Este resultado pode ser conferido no Wolfram aqui.
Qualquer dúvida esclareça no fórum.
Subscrever:
Mensagens (Atom)












.gif)