A matemática combinatória no Euromilhões

     , publicada por
Podemos pensar, que num caso hipotético poderiamos apostar em todas as combinações possíveis para o Euromilhões. E podíamos, mas mesmo se tivéssemos o dinheiro todo, vamos ver que nos sairia cara a ousadia.



No Euromilhões podemos apostar 5 números de entre 50, e duas estrelas de entre nove, sendo que cada aposta custa 2 euros. Vamos então às contas, ou seja, quanto custaria apostar em todas as combinações possíveis de forma a que tivéssemos a certeza absoluta que nos sairia o prémio?

Como não há repetição, ou seja, como não podemos escolher o mesmo número duas vezes, e a ordem não conta, ou seja, escolhermos primeiro o 1 e depois o 2, ou ao contrário é perfeitamente indiferente, estamos perante combinações.

Assim o número de combinações possíveis é:


Assim, há 76.275.360 casos possíveis para apostar no Euromilhões, se quisermos ter a certeza que ganhamos. Considerando 2€ para cada caso, ficamos então com 152.550.720€, ou seja cerca de 150 milhões de euros.

Considerando que o mair jackpot de sempre no Euromilhões foi de 180 milhões de euros, quando tal voltar a acontecer, pode ser um bom investimento, se tiver capital para tal, apostar em todos os casos possíveis. Concluindo, para ter 100% absoluta que ganha o Euromilhões, tinha de ser você o único apostador, não deixando mais ninguém apostar e tinha de gastar cerca de 150 milhões de euros. Se nessa semana o jackpot fosse de cerca de 180 milhões de euros, era investimento garantido.

No entanto, como raramente o prémio é superior a 150 milhões de euros, e as receitas das apostas andam perto ou acima desse valor, conclui-se facilmente que a organização sai sempre a ganhar.
5 comentários:

Tabela para transformadas de Laplace

     , publicada por
Já está disponível na Matemática Viva, uma tabela para transformadas de Laplace.

Contém as transformadas diretas e as transformadas inversas. Tem um número vasto de casos.

Descarregar aqui.

Agradecimentos a Tom Irvine
2 comentários:

Como calcular a primitiva de sen(sqrt(x)) ?

     , publicada por
Tentemos achar a seguinte primitiva:
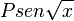
P sen{\sqrt{x}}
Usaremos o método da primitivação por substituição e da primitivação por partes.
Façamos a seguinte substituição: \sqrt{x}=t
Temos então que:
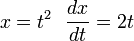
x=t^2 \ \ \frac{dx}{dt}=2t
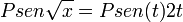
Substituindo ficamos então com: P sen{\sqrt{x}} = P sen{(t)}2t
Aplicamos agora a primitivação por partes
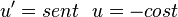
u'=sen{t} \ \ u=-cos{t}
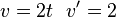
v=2t \ \ v'=2

Psen(t)2t = − cos(t)2t − P2( − cos(t)) = − cos(t)2t + 2Pcos(t) =
= − cos(t)2t + 2.sen(t) + C = 2( − t.cos(t) + sen(t)) + C
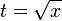fazendo agora a substituição inicial t=\sqrt{x} temos o resultado final: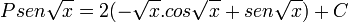

P sen{\sqrt{x}}=2(-\sqrt{x}.cos{\sqrt{x}}+sen{\sqrt{x}}) + C
Sem comentários:

O Explicador e a fiscalidade

     , publicada por
Se é explicador de qualquer matéria, e pretende cumprir a lei como é de saudar nos cidadãos que cumprem os seus deveres cívicos, terá de pagar impostos sobre as explicações que lecionar. Poderá trabalhar para uma empresa como trabalhador por conta de outrem como explicador, sendo que tudo o que receber ao fim do mês será líquido. No entanto tal é raro, normalmente o explicador trabalha por conta própria e como tal, se fizer dessa atividade a sua atividada única ou principal, deverá fazer os seus descontos para a Segurança Social e pagar IRS.

Deixo aqui algumas dicas então para a fiscalidade dos explicadores:

  • Segundo o n.º 11 do art.º 9.º do Código do IVA, os explicadores estão isentos de pagar IVA, o que é por si uma boa notícia. Ou seja, qualquer que sejam os seus rendimentos nunca terá de pagar IVA ao estado, nem de o cobrar aos seus explicandos.

  • Terá de pagar à Segurança Social, se quiser ter subsídio de parentalidade/maternidade, subsídio de invalidez, ou se quiser no futuro ter reforma. Com as novas leis da Segurança Social e com o memorando da tróica, os trabalhadores independentes, onde se incluem os explicadores, terão também direito a subsídio de doença e a subsídio de desemprego. Como tal é bastante recomendável que faça os seus descontos para a Segurança Social. Os descontos serão em função dos seus rendimentos. Encontra aqui uma aplicação muito simples que faz esse cálculo. Se fizer das explicações a sua segunda actividade, e trabalhar por conta de outrem na sua actividade principal, já alguém faz os seus descontos para a Segurança Social, sendo que em princípio não terá de os fazer você mesmo

  • Segundo o art. 9.º, n.º1 do DL n.º 42/91, de 22/1, está dispensado de fazer retenção na fonte se tiver redimentos anuais inferiores a 10000 Euros, ou seja se em explicações fizer em média menos que 834 Euros/mês

  • A categoria do explicador, tal como qualquer outro trabalhador independente, em sede de IRS é a categoria B. Sempre que receber um montante monetário de um aluno ou de um pai, deverá preencher um recibo verde com o montante recebido. De referir, o que é muito importante e vantajoso para o aluno ou para os pais, é que esse montante no recibo verde que você passar, será dedutível em sede de IRS em despesas de educação na folha de IRS do aluno ou dos pais.

  • O explicador, como apenas faz prestação de serviços, estará quase de certeza absoluta, sempre no Regime Simplificado, a não ser que tenha rendimentos em média de pelo menos 12500 Euros/mês. Tal é vantajoso para o explicador, pois no regime simplificado considera-se que do total dos rendimentos, 30% são para despesas, sendo que o explicador apesar de ter despesas, como livros, cadernos, canetas ou uma máquina de calcular de vez em quando, essas despesas são sempre muito menores que 30% dos seus rendimentos.

Em suma, existem uma série de benefícios fiscais para si, e para os seus clientes, sendo que se fizer das explicações a sua única actividade é de extrema importância pagar Segurança Social, se no futuro quiser ter direito a reforma. Qualquer dúvida não hesite em deixar comentários.
51 comentários:

Exercícios de Cálculo com solução da Faculdade de Ciências

     , publicada por
Já estão disponíveis na Matemática Viva, diversos exercícios de Cálculo, disciplina equivalente a Análise Matemática, desta vez, da disciplina da Faculdade de Ciências da Universidade de Lisboa. Este exercícios que têm solução, abordam seis capítulos:
  1. Números Reais
  2. Sucessões Reais
  3. Funções Reais de variável Real
  4. Cálculo Diferencial
  5. Primitivação
  6. Cálculo Integral
Os exercícios, assim como as respetivas soluções podem ser visto publicamente aqui.

Qualquer dúvida sobre quaisquer exercícios, respondemos gratuitamente no fórum.
2 comentários:

Exemplo no cálculo de uma exponencial matricial

     , publicada por



Imaginemos que queremos calcular eA sabendo que
A=\begin{bmatrix} 2 & 1 \\ 0 & 0 \end{bmatrix}
Calculemos A2,A3...An
A^{2}=\begin{bmatrix} 2 & 1 \\ 0 & 0 \end{bmatrix}\begin{bmatrix} 2 & 1 \\ 0 & 0 \end{bmatrix}=\begin{bmatrix} 4 & 2 \\ 0 & 0 \end{bmatrix}, A^{3}=A^{2}A=\begin{bmatrix} 8 & 4 \\ 0 & 0 \end{bmatrix}
A^{n}=\begin{bmatrix} 2^{n} & 2^{n-1} \\ 0 & 0 \end{bmatrix}, n\neq0
Sabemos então que
e^A=\sum_{n=0}^{\infty}\frac{A^n}{n!}
e^A=I+\sum_{n=1}^{\infty}\frac{A^n}{n!} = I+\sum_{n=1}^{\infty}\frac{1}{n!}\begin{bmatrix} 2^{n} & 2^{n-1} \\ 0 & 0 \end{bmatrix}=
= I+\begin{bmatrix} \sum_{n=1}^{\infty}\frac{2^{n}}{n!} & \sum_{n=1}^{\infty}\frac{2^{n-1}}{n!} \\ 0 & 0 \end{bmatrix}= \begin{bmatrix} \sum_{n=0}^{\infty}\frac{2^{n}}{n!} & \frac{1}{2}\sum_{n=1}^{\infty}\frac{2^{n}}{n!} \\ 0 & 1 \end{bmatrix}
e^A=\begin{bmatrix} e^2 & \frac{1}{2}(e^2-1) \\ 0 & 1 \end{bmatrix}
Sem comentários:

Considerações sobre os fractais

     , publicada por
Fractais são figuras da geometria com grande paralelismo com as figuras presentes na Natureza e no Universo, obtidos através de algoritmos matemáticos determinísticos ou estocásticos.
A geometria fractal é o ramo da matemática que estuda as propriedades e comportamento dos fractais. Descreve muitas situações que não podem ser explicadas facilmente pela geometria clássica, e foram aplicadas em ciência, tecnologia e arte gerada por computador. As raízes conceituais dos fractais remontam a tentativas de medir o tamanho de objetos para os quais as definições tradicionais baseadas na geometria euclidiana falham.
Um fractal (anteriormente conhecido como curva monstro) é um objeto geométrico que pode ser dividido em partes, cada uma das quais semelhante ao objeto original. Diz-se que os fractais têm infinitos detalhes, são geralmente autossimilares e independem de escala. Em muitos casos um fractal pode ser gerado por um padrão repetido, tipicamente um processo recorrente ou iterativo.
O termo foi criado em 1975 por Benoît Mandelbrot, matemático francês nascido na Polónia, que descobriu a geometria fractal na década de 1970 do século XX, a partir do adjetivo latino fractus, do verbo frangere, que significa quebrar.
Vários tipos de fractais foram originalmente estudados como objetos matemáticos.

História

Floco de neve de Koch
Durante séculos, os objetos e os conceitos da filosofia e da geometria euclidiana foram considerados como os que melhor descreviam o mundo em que vivemos. A descoberta de geometrias não-euclidianas introduziu novos objetos que representam certos fenômenos do Universo, tal como se passou com os fractais. Assim, considera-se hoje que tais objetos retratam formas e fenômenos da Natureza.
A ideia dos fractais teve a sua origem no trabalho de alguns cientistas entre 1857 e 1913. Esse trabalho deu a conhecer alguns objetos, catalogados como "demônios", que se supunha não terem grande valor científico.
Em 1872, Karl Weierstrass encontrou o exemplo de uma função com a propriedade de ser contínua em todo seu domínio, mas em nenhuma parte diferenciável. O gráfico desta função é chamado atualmente de fractal. Em 1904, Helge von Koch, não satisfeito com a definição muito abstrata e analítica de Weierstrass, deu uma definição mais geométrica de uma função similar, atualmente conhecida como Koch snowflake (ou floco de neve de Koch), que é o resultado de infinitas adições de triângulos ao perímetro de um triângulo inicial. Cada vez que novos triângulos são adicionados, o perímetro cresce, e fatalmente se aproxima do infinito. Dessa maneira, o fractal abrange uma área finita dentro de um perímetro infinito.
Também houve muitos outros trabalhos relacionados a estas figuras, mas esta ciência só conseguiu se desenvolver plenamente a partir da década de 1960, com o auxílio da computação. Um dos pioneiros a usar esta técnica foi Benoît Mandelbrot, um matemático que já vinha estudando tais figuras. Mandelbrot foi responsável por criar o termo fractal, e responsável pela descoberta de um dos fractais mais conhecidos, o conjunto de Mandelbrot.

Categorias de fractais

A conjunto inteiro de Mandelbrot
Ampliado 4x
Ampliado 30x
Zoomed 350xAumento de 350 vezes do conjunto de Mandelbrot mostra os pequenos detalhes repetindo o conjunto inteiro.
Os fractais podem ser agrupados em três categorias principais. Estas categorias são determinadas pelo modo como o fractal é formado ou gerado:
  • Sistema de funções iteradas — Estas possuem uma regra fixa de substituição geométrica. Conjunto de Cantor, tapete de Sierpinski, Sierpinski gasket, curva de Peano, floco de neve de Koch, curva do dragão de Harter-Heighway, T-Square,esponja de Menger, são alguns exemplos deste tipo de fractal.
  • Fractais definidos por uma relação de recorrência em cada ponto do espaço (tal como o plano complexo). Exemplos deste tipo são o conjunto de Mandelbrot e o fractal de Lyapunov. Estes também são chamados de fractais de fuga do tempo.
  • Fractais aleatórios, gerados por processos estocásticos ao invés de determinísticos, por exemplo, terrenos fractais e ovôo de Lévy.
Ainda, também podem ser classificados de acordo com sua autossimilaridade. Existem três tipos de autossimilaridade encontrados em fractais:
  • Autossimilaridade exata: é a forma em que a autossimilaridade é mais marcante, evidente. O fractal é idêntico em diferentes escalas. Fractais gerados por sistemas de funções iterativas geralmente apresentam uma autossimilaridade exata.
  • Quase-autossimilaridade: é uma forma mais solta de autossimilaridade. O fractal aparenta ser aproximadamente (mas não exatamente) idêntico em escalas diferentes. Fractais quase-autossimilares contém pequenas cópias do fractal inteiro de maneira distorcida ou degenerada. Fractais definidos por relações de recorrência são geralmente quase-autossimilares, mas não exatamente autossimilares.
  • Autossimilaridade estatística: é a forma menos evidente de autossimilaridade. O fractal possui medidas númericas ou estatísticas que são preservadas em diferentes escalas. As definições de fractais geralmente implicam alguma forma de autossimilaridade estatística (mesmo a dimensão fractal é uma medida numérica preservada em diferentes escalas). Fractais aleatórios são exemplos de fractais que possuem autossimilaridade estatística, mas não são exatamente nem quase autossimilares.
Entretanto, nem todos os objetos autossimilares são considerados fractais. Uma linha real (uma linha reta Euclidiana), por exemplo, é exatamente autossimilar, mas o argumento de que objetos Euclidianos são fractais é defendido por poucos. Mandelbrot argumentava que a definição de fractal deveria incluir não apenas fractais "verdadeiros" mas também objetos Euclidianos tradicionais, pois números irracionais em uma linha real representam propriedades complexas e não repetitivas.
Pelo fato do fractal possuir uma granulometria infinita, nenhum objeto natural pode sê-lo. Os objetos naturais podem exibir uma estrutura semelhante ao fractal, porém com uma estrutura de tamanho limitado.

Um conjunto de Julia, um fractal relacionado ao conjunto Mandelbrot

Um brócolis como exemplo de um belo fractal natural.

Uma animação com uma fractal que modela a superfície de uma montanha

Duas folhas de acrílico cobertas de cola, quando espremidas formam um fractal natural

Uma perturbação causada por alta tensãoem um bloco de acrílico cria um fractalAgregação por difusão limitada.
.

Fractal conjunto de Julia
Sem comentários:

Considerações matemáticas sobre o número de Euler

     , publicada por
Na matemática , número de Euler (pronuncia-se óilar), assim chamado em homenagem ao matemático suíço Leonhard Euler, é a base dos logaritmos naturais. As variantes do nome do número incluem: número de Napier,constante de Néper, número neperiano, constante matemática e número exponencial, etc. A primeira referência à constante foi publicada em 1618 na tabela de um apêndice de um trabalho sobre logaritmos de John Napier. No entanto, este não contém a constante propriamente dita, mas apenas uma simples lista de logaritmos naturais calculados a partir desta. A primeira indicação da constante foi descoberta por Jakob Bernoulli, quando tentava encontrar um valor para a seguinte expressão (muito comum no cálculo de juros compostos):
k{e}^{r} = \lim_{n\to\infty} \left(k\left(1+\frac{r}{n}\right)^n\right)
para r = k = 1, ou seja:
e = \lim_{n\to\infty} \left(1+\frac{1}{n}\right)^n
ou ainda, substituindo-se n por \frac{1}{h}
e = \lim_{h\to 0} \left(1+h\right)^\frac{1}{h}
,cujo valor é aproximadamente 2,718 281 828 459 045 235 360 287.

Caracterizações menos triviais do número de Euler

Alternativamente à representação mais conhecida, temos também:  \lim_{x \rightarrow 0^{+}} (1+x)^{\frac{1}{x}} = e
O número e pode ser representado e calculado por meio da utilização da série de Taylor para ex quando x=1, como a soma da seguinte série infinita:
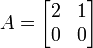
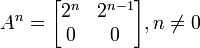
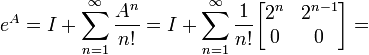
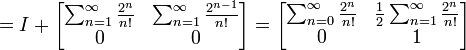
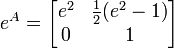
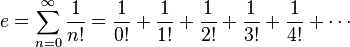
e = \sum_{n=0}^\infty {1 \over n!} = {1 \over 0!} + {1 \over 1!} + {1 \over 2!} + {1 \over 3!} + {1 \over 4!} + \cdots
Aqui n! representa o factorial de n.
A função ex (função exponencial de base e) pode ser representada da seguinte forma:
(\forall x\in\mathbb{R}), exp(x) = ex
assim, por exemplo, tem-se :
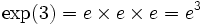\exp(3)=e\times e \times e=e^3 ou ainda
\exp(-4)=\frac{1}{e}\times \frac{1}{e}\times \frac{1}{e}\times \frac{1}{e}=\left(\frac{1}{e}\right)^4=e^{-4}
Outra maneira de se encontrar o valor de e é pelo desenvolvimento da fração contínua, escrito sob a forma interessante:
e=2+\frac{1}{1+\frac{1}{2+\frac{1}{1+\frac{1}{1+\frac{1}{4+\frac{1}{1+\frac{1}{1+\frac{1}{6+\ldots}}}}}}}}
Ou, de forma mais simplificada:
e = [[2; 1, \textbf{2}, 1, 1, \textbf{4}, 1, 1, \textbf{6}, 1, 1, \textbf{8}, 1, 1, \ldots, \textbf{2n}, 1, 1, \ldots]], \,
que pode ser escrita mais harmoniozamente com a utilização do zero:
e = [[ 1 , \textbf{0} , 1 , 1, \textbf{2}, 1, 1, \textbf{4}, 1 , 1 , \textbf{6}, 1, 1, \textbf{8}, 1, 1, \ldots]], \,
Muitas outras séries, sequências, frações contínuas e produtos infinitos que representam e já foram desenvolvidas.

O Número de Euler no Cálculo

A função exponencial y = ex tem a intrigante propriedade de ser sua própria derivada, i.e.:
\frac{d}{dx}e^{x}=e^{x}
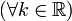Isto significa que e tem a notável propriedade de que a taxa de variação de ex no ponto x = t vale et. Daí sua importância no cálculo diferencial e integral, e seu papel único como base do logaritmo natural. Além desta, pela regra da multiplicação por constante, as funções y = kex, (\forall k\in\mathbb{R}) também são suas próprias derivadas.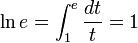
Trabalhando com integrais, pode-se ainda definir e como sendo o único número maior que zero tal que:
\ln{e} = \int_{1}^{e} \frac{dt}{t} = {1}


Mais Sobre o número de Euler

O número e é um número irracional e mesmo transcendente (como pi). A irracionalidade de e foi demonstrada por Lambert em 1761 e mais tarde por Euler. A prova da transcendência de e foi estabelecida por Hermite em 1873.
Conjecturou-se que e é um número normal ou aleatório.
Ele aparece (com outras constantes fundamentais) na identidade de Euler, considerada a expressão mais "bela" da matemática:
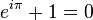
e^{i\pi}+1=0 \,
Obtém-se tal relação por meio da fórmula:
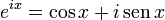
e^{ix} = \cos x + i\,\text{sen}\,x \,\!
que, por sua vez, advém da série de Taylor para f(ix) = eix.
Leonhard Euler começou a usar a letra e para representar a constante em 1727, e o primeiro uso de e foi na publicação Euler’s Mechanica (1736). As verdadeiras razões para escolha da letra são desconhecidas, mas especula-se que seja porque e é a primeira letra da palavra exponencial.
Outra aparição do número de Euler é na probabilidade: caso se escolham números entre zero e 1 até que o seu total ultrapasse 1, o número mais provável de seleções será igual a e.

Nas séries infinitas

Dentre as várias séries infinitas que resultam em e, têm-se, além da trivial:
e = \left [ \sum_{k=0}^\infty \frac{(-1)^k}{k!} \right ]^{-1}
e = \left [ \sum_{k=0}^\infty \frac{1-2k}{(2k)!} \right ]^{-1}
e = \frac{1}{2} \sum_{k=0}^\infty \frac{k+1}{k!}
e = 2 \sum_{k=0}^\infty \frac{k+1}{(2k+1)!}
e = \sum_{k=0}^\infty \frac{3-4k^2}{(2k+1)!}
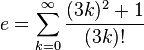
e = \sum_{k=0}^\infty \frac{(3k)^2+1}{(3k)!}
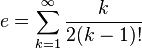
e = \sum_{k=1}^\infty \frac{k}{2(k-1)!}
e = \sum_{k=1}^\infty \frac{k^2}{2(k!)}
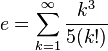
e = \sum_{k=1}^\infty \frac{k^3}{5(k!)}
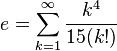
e = \sum_{k=1}^\infty \frac{k^4}{15(k!)}

 Nos limites e produtos infinitos

Os produtos infinitos
e= 2 \left ( \frac{2}{1} \right )^{1/2} \left ( \frac{2}{3}\; \frac{4}{3} \right )^{1/4} \left ( \frac{4}{5}\; \frac{6}{5}\; \frac{6}{7}\; \frac{8}{7} \right )^{1/8} \cdots
e
e = \left ( \frac{2}{1} \right )^{1/1} \left (\frac{2^2}{1 \cdot 3} \right )^{1/2} \left (\frac{2^3 \cdot 4}{1 \cdot 3^3} \right )^{1/3} \left (\frac{2^4 \cdot 4^4}{1 \cdot 3^6 \cdot 5} \right )^{1/4} \cdots ,
, em que o n-ésimo factor corresponde à raiz do produto
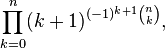
\prod_{k=0}^n (k+1)^{(-1)^{k+1}{n \choose k}},
resultam no número de Euler, assim como os seguintes limites:
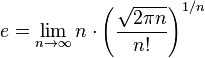
e= \lim_{n \to \infty} n\cdot\left ( \frac{\sqrt{2 \pi n}}{n!} \right )^{1/n}
e=\lim_{n \to \infty} \frac{n}{\sqrt[n]{n!}}
e=\lim_{n \to \infty} \left [ \frac{(n+1)^{n+1}}{n^n}- \frac{n^n}{(n-1)^{n-1}} \right ]
O Número de Euler com os primeiros 510 dígitos decimais

e=2{,}718\;281\;828\;459\;045\;235\;360\;287\;471\;352\;662\;497\;757\;247
\;093\;699\;959\;574\;966\;967\;627\;724\;076\;630\;353\;547\;594\;571\;382
\;178\;525\;166\;427\;427\;466\;391\;932\;003\;059\;921\;817\;413\;596\;629
\;043\;572\;900\;334\;295\;260\;595\;630\;738\;132\;328\;627\;943\;490\;763
\;233\;829\;880\;753\;195\;251\;019\;011\;573\;834\;187\;930\;702\;154\;089
\;149\;934\;884\;167\;509\;244\;761\;460\;668\;082\;264\;800\;168\;477\;411
\;853\;742\;345\;442\;437\;107\;539\;077\;744\;992\;069\;551\;702\;761\;838
\;606\;261\;331\;384\;583\;000\;752\;044\;933\;826\;560\;297\;606\;737\;113
\;200\;709\;328\;709\;127\;443\;747\;047\;230\;696\;977\;209\;310\;141\;692
\;836\;819\;025\;515\;108\;657\;463\;772\;111\;252\;389\;784\;425\;056\;953
\;696\;770\;785\;449\;969\;967\;946\;864\;454\;905\;987\;931\;636\;889\;230
\;098\;793\;127\;736\;178\;215\;4\,\ldots
3 comentários:
Subscrever: Mensagens (Atom)