Na matemática , número de Euler (pronuncia-se óilar), assim chamado em homenagem ao matemático suíço Leonhard Euler, é a base dos logaritmos naturais. As variantes do nome do número incluem: número de Napier,constante de Néper, número neperiano, constante matemática e número exponencial, etc. A primeira referência à constante foi publicada em 1618 na tabela de um apêndice de um trabalho sobre logaritmos de John Napier. No entanto, este não contém a constante propriamente dita, mas apenas uma simples lista de logaritmos naturais calculados a partir desta. A primeira indicação da constante foi descoberta por Jakob Bernoulli, quando tentava encontrar um valor para a seguinte expressão (muito comum no cálculo de juros compostos):
para r = k = 1, ou seja:
ou ainda, substituindo-se n por 

,cujo valor é aproximadamente 2,718 281 828 459 045 235 360 287.
Caracterizações menos triviais do número de Euler
Alternativamente à representação mais conhecida, temos também: 

O número e pode ser representado e calculado por meio da utilização da série de Taylor para ex quando x=1, como a soma da seguinte série infinita:
Aqui n! representa o factorial de n.
A função ex (função exponencial de base e) pode ser representada da seguinte forma:
 , exp(x) = ex
, exp(x) = ex
assim, por exemplo, tem-se :
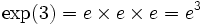 ou ainda
ou ainda
Outra maneira de se encontrar o valor de e é pelo desenvolvimento da fração contínua, escrito sob a forma interessante:
Ou, de forma mais simplificada:
que pode ser escrita mais harmoniozamente com a utilização do zero:
Muitas outras séries, sequências, frações contínuas e produtos infinitos que representam e já foram desenvolvidas.
O Número de Euler no Cálculo
A função exponencial y = ex tem a intrigante propriedade de ser sua própria derivada, i.e.:
Isto significa que e tem a notável propriedade de que a taxa de variação de ex no ponto x = t vale et. Daí sua importância no cálculo diferencial e integral, e seu papel único como base do logaritmo natural. Além desta, pela regra da multiplicação por constante, as funções y = kex,  também são suas próprias derivadas.
também são suas próprias derivadas.
 também são suas próprias derivadas.
também são suas próprias derivadas.Trabalhando com integrais, pode-se ainda definir e como sendo o único número maior que zero tal que:
Mais Sobre o número de Euler
O número e é um número irracional e mesmo transcendente (como pi). A irracionalidade de e foi demonstrada por Lambert em 1761 e mais tarde por Euler. A prova da transcendência de e foi estabelecida por Hermite em 1873.
Conjecturou-se que e é um número normal ou aleatório.
Ele aparece (com outras constantes fundamentais) na identidade de Euler, considerada a expressão mais "bela" da matemática:
Obtém-se tal relação por meio da fórmula:
que, por sua vez, advém da série de Taylor para f(ix) = eix.
Leonhard Euler começou a usar a letra e para representar a constante em 1727, e o primeiro uso de e foi na publicação Euler’s Mechanica (1736). As verdadeiras razões para escolha da letra são desconhecidas, mas especula-se que seja porque e é a primeira letra da palavra exponencial.
Outra aparição do número de Euler é na probabilidade: caso se escolham números entre zero e 1 até que o seu total ultrapasse 1, o número mais provável de seleções será igual a e.
Nas séries infinitas
Dentre as várias séries infinitas que resultam em e, têm-se, além da trivial:
Nos limites e produtos infinitos
Os produtos infinitos
e
, em que o n-ésimo factor corresponde à raiz do produto
resultam no número de Euler, assim como os seguintes limites:
- O Número de Euler com os primeiros 510 dígitos decimais
-




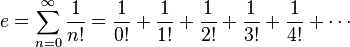

![e = [[2; 1, \textbf{2}, 1, 1, \textbf{4}, 1, 1, \textbf{6}, 1, 1, \textbf{8}, 1, 1, \ldots, \textbf{2n}, 1, 1, \ldots]], \,](https://upload.wikimedia.org/math/b/f/c/bfc5c0fc52a8ea49c5e4ee8defd1669b.png)
![e = [[ 1 , \textbf{0} , 1 , 1, \textbf{2}, 1, 1, \textbf{4}, 1 , 1 , \textbf{6}, 1, 1, \textbf{8}, 1, 1, \ldots]], \,](https://upload.wikimedia.org/math/9/7/8/97826412eb1f18fbf233a3227e73cd9c.png)

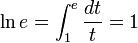
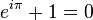
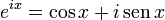
![e = \left [ \sum_{k=0}^\infty \frac{(-1)^k}{k!} \right ]^{-1}](https://upload.wikimedia.org/math/a/e/e/aee6e89e7dadfca2d0f4ab8ef07da7e2.png)
![e = \left [ \sum_{k=0}^\infty \frac{1-2k}{(2k)!} \right ]^{-1}](https://upload.wikimedia.org/math/3/4/7/347be98b47bdc3e043fe243d36c189c9.png)



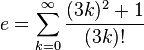
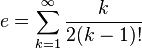

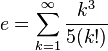
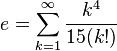


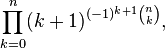
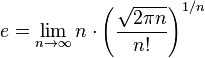
![e=\lim_{n \to \infty} \frac{n}{\sqrt[n]{n!}}](https://upload.wikimedia.org/math/1/e/c/1ece0ee65e250a7a3ec0a38140ef258c.png)
![e=\lim_{n \to \infty} \left [ \frac{(n+1)^{n+1}}{n^n}- \frac{n^n}{(n-1)^{n-1}} \right ]](https://upload.wikimedia.org/math/a/5/a/a5a7a2f503a54c1cfaf249f1fa146ebc.png)
Este comentário foi removido por um gestor do blogue.
ResponderEliminarcopy paste da wikipedia, muito bom...
ResponderEliminarOlá. É verdade, não o nego. O que vc não sabe é que eu contribuo muito em artigos matemáticos para a wikipedia, e depois copio alguns artigos para aqui.
ResponderEliminarhttp://pt.wikipedia.org/wiki/Usu%C3%A1rio:Joao.pimentel.ferreira
atentamente