Considerações matemáticas sobre o PI

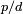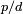Na matemática, $\scriptstyle{\pi}$ é uma proporção numérica originada da relação entre as grandezas do perímetro de uma circunferência e seu diâmetro; por outras palavras, se uma circunferência tem perímetro $\scriptstyle p$ e diâmetro $\scriptstyle d$ , então aquele número é igual a $\scriptstyle p/d$ . É representado pela letra grega π. A letra grega π (lê-se: pi), foi adoptada para o número a partir da palavra grega para perímetro, "περίμετρος", provavelmente por William Jones em 1706, e popularizada por Leonhard Euler alguns anos mais tarde. Outros nomes para esta constante são constante circular, constante de Arquimedes ou número de Ludolph.

Notação

Os primeiros a utilizarem a letra grega $\scriptstyle{\pi}$ foram os matemáticos ingleses, mas para designar a circunferência de um círculo. O primeiro a utilizar definição atual foi William Jones. Entretanto foi só após Leonhard Euler utilizá-la que houve aceitação da notação pela comunidade científica.

Valor de $π$

O valor de

π

pertence aos números irracionais. Para a maioria dos cálculos simples é comum aproximar

π

por 3,14. Uma boa parte das calculadoras científicas de 8 dígitos aproxima

π

por 3,1415927. Para cálculos mais precisos pode-se utilizar 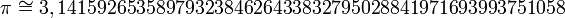$\pi \cong 3,1415926535897932384626433832795028841971693993751058$ com 52 casas decimais. Para cálculos ainda mais precisos pode-se obter aproximações de

π

através de algoritmos computacionais.

Aproximações para $π$

Desde a Antiguidade, foram encontradas várias aproximações de

π

para o cálculo da área do círculo. Entre os egípcios, por exemplo no papiro de Ahmes, o valor atribuído a

π

seria $\scriptstyle \left ( \frac{4}{3} \right )^3$ , embora também seja encontrado o valor $\scriptstyle 3 \frac{1}{6}$ . Na Bíblia (1 Reis 7:23) é possível encontrar que os hebreus utilizavam o valor 3 como aproximação de

π

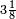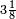. Entre os babilónios, era comum o uso do valor 3 para calcular a área do círculo, apesar de o valor $\scriptstyle 3 \frac{1}{8}$ já ser conhecido como aproximação.

Métodos de cálculo

Existem muitas formas de se obter o valor exato de

π

e alguns métodos aproximados. Consideramos que [[

π

]] é um número irracional e transcendente, de forma que os métodos de cálculo sempre envolvem aproximações, aproximações sucessivas e/ou séries infinitas de somas, multiplicações e divisões.

Método clássico para o cálculo de $π$

Método do clássico para o cálculo de

π

A primeira tentativa rigorosa de encontrar

π

deve-se a um dos mais conhecidos matemáticos da Antiguidade, Arquimedes. Pela construção de polígonos inscrito e circunscrito de 96 lados encontrou que pi seria entre um valor entre 223/71 e 22/7, ou seja, estaria aproximadamente entre 3,1408 e 3,1429. Tal método é o chamado método clássico para cálculo de pi.

Ptolomeu, que viveu em Alexandria aproximadamente no século III d.C., calculou pi tomando por base um polígono de 720 lados inscrito numa circunferência de 60 unidades de raio. Seu valor foi aproximadamente 3,1416. Considerando o que sabemos atualmente, sua aproximação foi bem melhor que a de Arquimedes.

A "busca" pelo valor de

π

chegou até à China, onde Liu Hui, um copiador de livros, conseguiu obter o valor 3,14159 com um polígono de 3.072 lados. Mas só no final do século V que o matemático Tsu Ch'ung-chih chegou a uma aproximação melhor: entre 3,1415926 e 3,1415927.

Nesta mesma época, o matemático hindu Aryabhata deixou registrado em versos num livro a seguinte afirmação: "Some-se 4 a 100, multiplique-se por 8 e some-se 62.000. O resultado é aproximadamente uma circunferência de diâmetro 20.000".

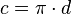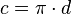Analisando matematicamente e considerando a equação citada anteriormente de $c = \pi \cdot d$ :

$(4 + 100) \cdot 8 + 62000 \approx \pi \cdot 20000 \Rightarrow$

$104 \cdot 8 + 62000 \approx \pi \cdot 20000 \Rightarrow$

$832 + 62000 \approx \pi \cdot 20000 \Rightarrow$

$62832 \approx \pi \cdot 20000 \Rightarrow$

${62832 \over 20000} \approx \pi$

O valor de

π

, portanto, seria 3,1416. Obviamente, quanto maior o número de casas decimais, melhor a aproximação do valor real de pi. Mas devemos considerar que, na época, isso não era algo fácil de se calcular.

O maior cálculo de casas decimais até o século XV foi 3,1415926535897932 feito pelo matemático árabe al-Kashi. O matemático holandês Ludolph van Ceulen, no final do século XVI, calculou um valor de

π

com 35 casas decimais, começando com um polígono de 15 lados, dobrando o número de lados 37 vezes, e, logo em seguida, aumentando o número de lados. Por curiosidade, a sua esposa mandou gravar no seu túmulo o valor de

π

com as supracitadas 35 casas decimais.

Hoje em dia é relativamente mais fácil, com os computadores modernos que calculam até bilhões de casas decimais para

π

Uma aproximação de

π

que apresenta diferença de aproximadamente 2,7e-7 é a seguinte:

${355 \over 113} \approx \pi$

A Matemática Viva

Abstracta, racional, por vezes intuitiva, sempre filosófica a matemática é a ferramenta fundamental desde os tempos primordiais. Desde tempos imemoráveis que o Homem faz uso da matemática para auxílio ao seu quotidiano.

Mas desde quando na evolução humana, começou a nossa espécie a tecer raciocínios abstractos matemáticos? Foi um passo bastante longo, moroso, mas foi um passo deveras importantíssimo na evolução do Homem; muito mais relevante que a invenção do fogo ou da roda. O raciocínio abstracto é o que nos difere das outras espécies, para os crentes é uma dádiva divina que nos diferencia e nos torna superiores, para os incrédulos e laicos é somente um passo evolutivo devido às necessidades dos tempos e talvez mesmo por questões de sobrevivência.

O que é certo é que a Matemática, e posteriormente a Filosofia e as Artes talvez tenham sido as primeiras ferramentas que o Homem concebeu com a sua capacidade de abstracção.

Já na nossa era, os matemáticos tentaram-nos incutir uma Matemática extremamente racional e abstracta, muitas vezes sem quaisquer paralelismos com o mundo terreno. Talvez uma premonição, mas o que é certo é que o número um surgiu para representar um objecto físico.

A matemática surgiu como uma necessidade do Homem no seu trajecto evolutivo, à medida que aumentava o seu volume craniano, foi sendo dotado de raciocínios algébricos. Se o Pensamento foi uma dádiva de Deus ou uma necessidade não o sabemos, mas é este que fez o Homem evoluir, é este que nos diferencia das outras espécies, foi este que nos levou a Marte, que criou a roda, e que nos fornece todas as panóplias quer frívolas, quer de grande utilidade, do nosso mundo moderno.

A Matemática é Viva quando é processada por seres humanos, quando é intuitiva, quando a sentimos útil aos nosso pressupostos. Aliemos então a Matemática, supostamente estritamente pura implicando assim ser apenas racional, à criatividade e sensibilidade humanas. É esta união que torna a Matemática elegante

Sendo elegante,
A Matemática é Viva quando é Humana