significa que f(x) se aproxima tanto de L quanto quisermos, quando se toma x suficientemente próximo de c. Quando tal acontece dizemos que "o limite def(x), à medida que x se aproxima de c, é L". Note-se que esta afirmação pode ser verdadeira mesmo quando 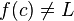 , ou quando a função f(x) nem sequer está definida em c. Vejamos dois exemplos que ajudam a ilustrar estes dois pontos importantíssimos.
, ou quando a função f(x) nem sequer está definida em c. Vejamos dois exemplos que ajudam a ilustrar estes dois pontos importantíssimos.
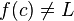 , ou quando a função f(x) nem sequer está definida em c. Vejamos dois exemplos que ajudam a ilustrar estes dois pontos importantíssimos.
, ou quando a função f(x) nem sequer está definida em c. Vejamos dois exemplos que ajudam a ilustrar estes dois pontos importantíssimos.Consideremos 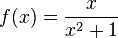 à medida que x se aproxima de 2. Neste caso, f(x) está definido em 2 e é igual ao seu limite: 0.4, vejamos:
à medida que x se aproxima de 2. Neste caso, f(x) está definido em 2 e é igual ao seu limite: 0.4, vejamos:
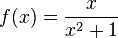 à medida que x se aproxima de 2. Neste caso, f(x) está definido em 2 e é igual ao seu limite: 0.4, vejamos:
à medida que x se aproxima de 2. Neste caso, f(x) está definido em 2 e é igual ao seu limite: 0.4, vejamos:| f(1.9) | f(1.99) | f(1.999) | f(2) | f(2.001) | f(2.01) | f(2.1) |
| 0.4121 | 0.4012 | 0.4001 |  0.4 0.4 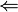 | 0.3998 | 0.3988 | 0.3882 |
À medida que x aproxima-se de 2, f(x) aproxima-se de 0.4 e consequentemente temos a igualdade  . Sempre que se verifique a igualdade
. Sempre que se verifique a igualdade 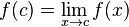 , diz-se que f é contínua em x = c. A igualdade não é válida para todas as funções. Vejamos uma função onde tal não acontece
, diz-se que f é contínua em x = c. A igualdade não é válida para todas as funções. Vejamos uma função onde tal não acontece
 . Sempre que se verifique a igualdade
. Sempre que se verifique a igualdade 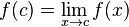 , diz-se que f é contínua em x = c. A igualdade não é válida para todas as funções. Vejamos uma função onde tal não acontece
, diz-se que f é contínua em x = c. A igualdade não é válida para todas as funções. Vejamos uma função onde tal não aconteceO limite de g(x) à medida que x se aproxima de 2 é 0.4 (tal como em f(x)), mas 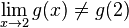 e consequentemente g não é contínua em x = 2.
e consequentemente g não é contínua em x = 2.
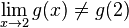 e consequentemente g não é contínua em x = 2.
e consequentemente g não é contínua em x = 2.Consideremos agora o caso onde f(x) não está definida em x = c.
Apesar de f(x) não estar definida em x = 1, o limite de f(x), quando x se aproxima de 1, existe e é igual a 2:
| f(0.9) | f(0.99) | f(0.999) | f(1.0) | f(1.001) | f(1.01) | f(1.1) |
| 1.95 | 1.99 | 1.999 |  não está definido não está definido 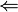 | 2.001 | 2.010 | 2.10 |
Ora x pode ser tomado tão próximo de 1 quanto quisermos, sem no entanto ser 1, pelo que o limite de f(x) é 2.

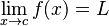
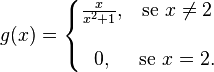
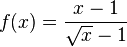
Sem comentários:
Enviar um comentário